Combinatorial & Simulation-Based Optimization

Combinatorial problems arise in many domains and involve finding a suitable solution out of a huge, but finite solution space. Many well-known problems can be categorized into selection, assignment, ordering, and grouping problems as depicted below. In general, combinatorial optimization involves a number of variables with a finite domain and a solution consists of a concrete element picked for each variable from the domain.

Practical applications of combinatorial optimization include production planning, tour planning, truck door assignment, graph coloring, scheduling, and more. Typically, in an applied research project we start by identifying the type of problem that needs to be solved and derive a (mathematical) program to describe the objectives and constraints. Then we evaluate existing solution techniques to find optimal or near-optimal solutions, or, if existing techniques do not suffice, develop new techniques that are specific to the given problem.

Assignment problems

Solving assignment problems requires to find the best mapping between two finite sets of items. The solution space is mainly described by the cardinalities that are possible in the assignment. The cardinalities on both sides can indicate optionality, identity, and multiplicity. Multiple items of one set may be assigned to one or even multiple items of the other set. Soemtimes even, not all items of one or both sets need to be mapped. Assignment is a very general problem description, so that many of the other problem types could be represented as an assignment problem. For instance, selection could be represented as an assignment between a second set with two items: selected and discarded.

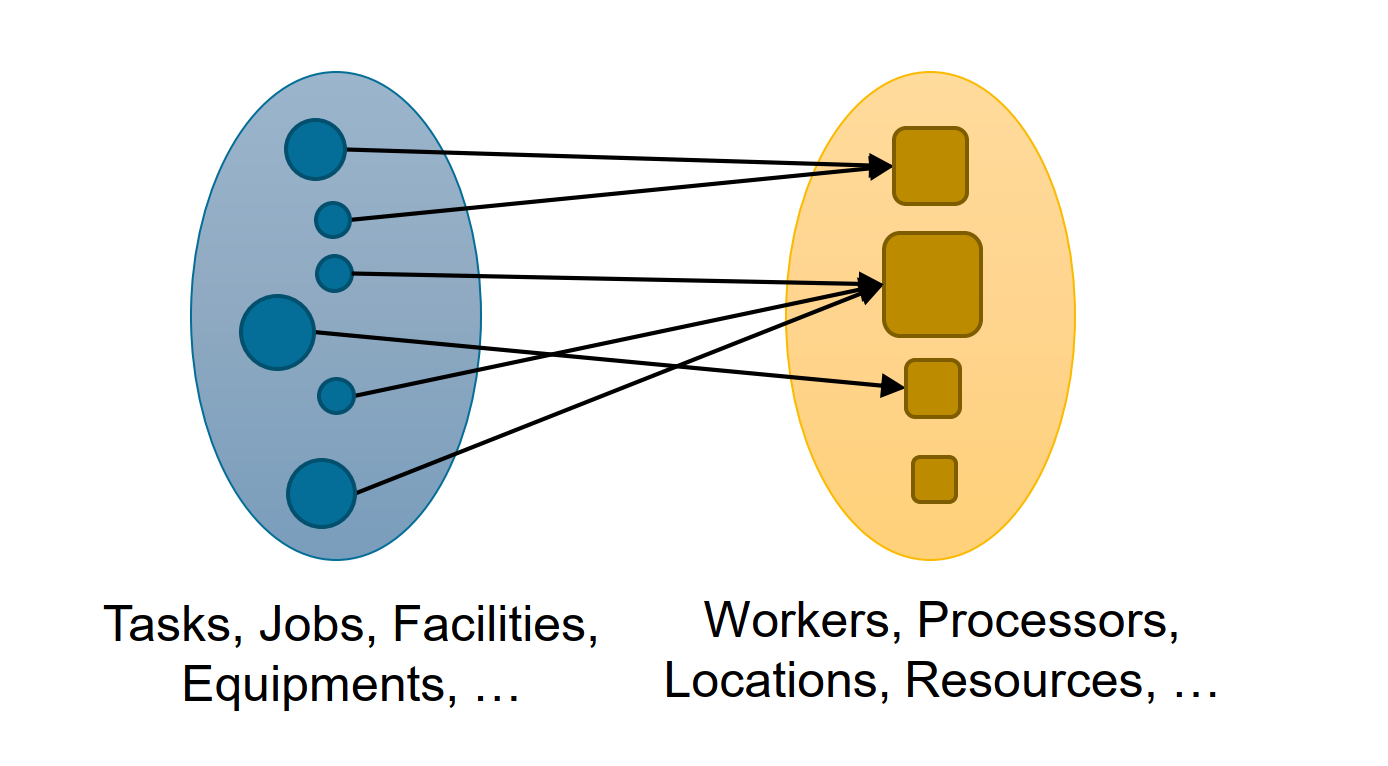
Well-known problems: linear assignment problem (LAP), quadratic assignment problem (QAP), generalized assignment problem (GAP), generalized quadratic assignment problem (GQAP)

Ordering problems

Solving an ordering problem requires to find the best order of a number of given finite set of items, e.g. N customers. For instance, the customers that have to be visited in a tour, or the jobs that have to be produced on a certain machine. The search space of such problems can be described in general by a permutation of the items and thus if of size N!. Solution spaces may be slightly smaller as sometimes there are symmetries, for instance when all distances between customers are equally large in both directions or when there are jobs that have the same properties. In addition, it can be the case that the order forms a cycle and that only the relative positioning of items is important and not the absolute position in the sequence.

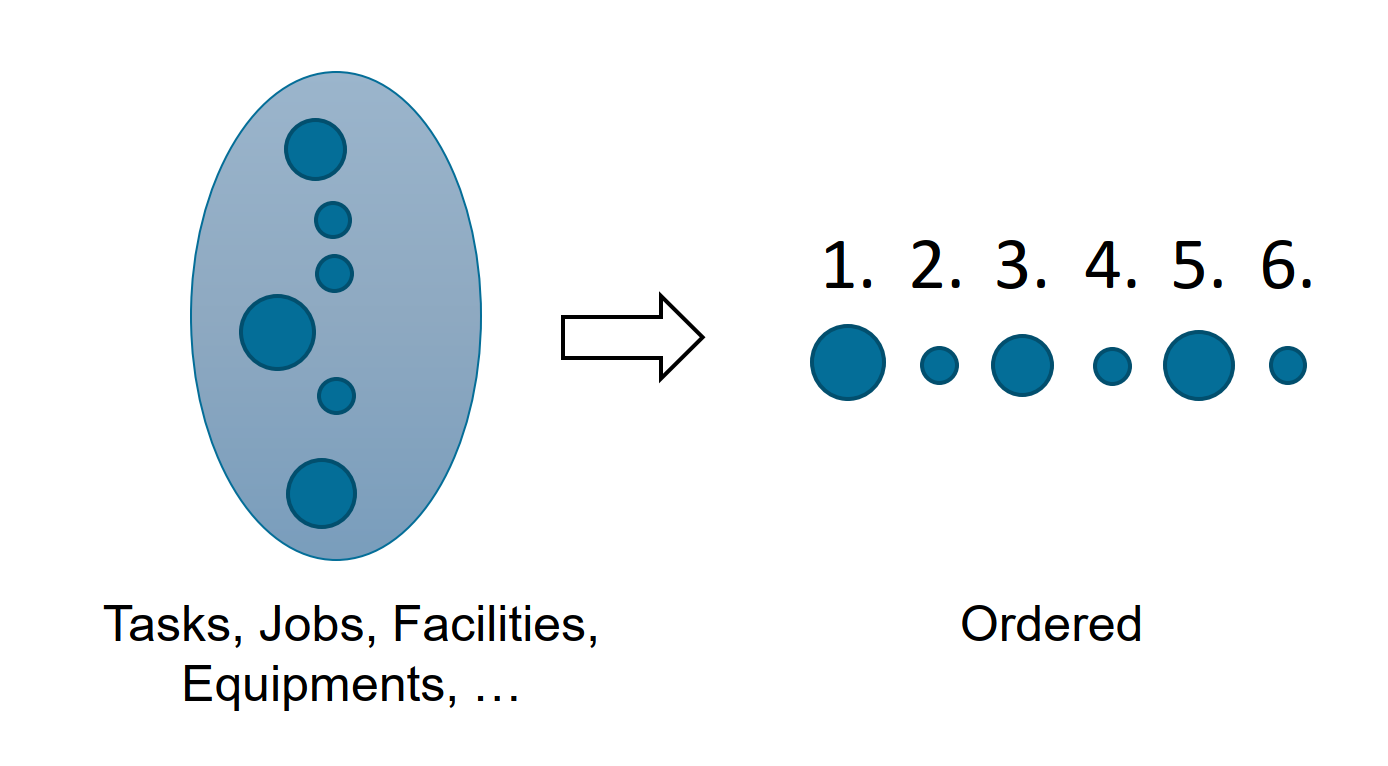
Well-known problems: traveling salesman problem (TSP), single-machine scheduling problem

Selection problems

Solving selection problems requires to find a subset of a set of items. Thereby, variations of the problem occur whether an item may be selected multiple times or just once. The selected set of items constitutes the solution and may for instance denote a set of projects that should be invested in.

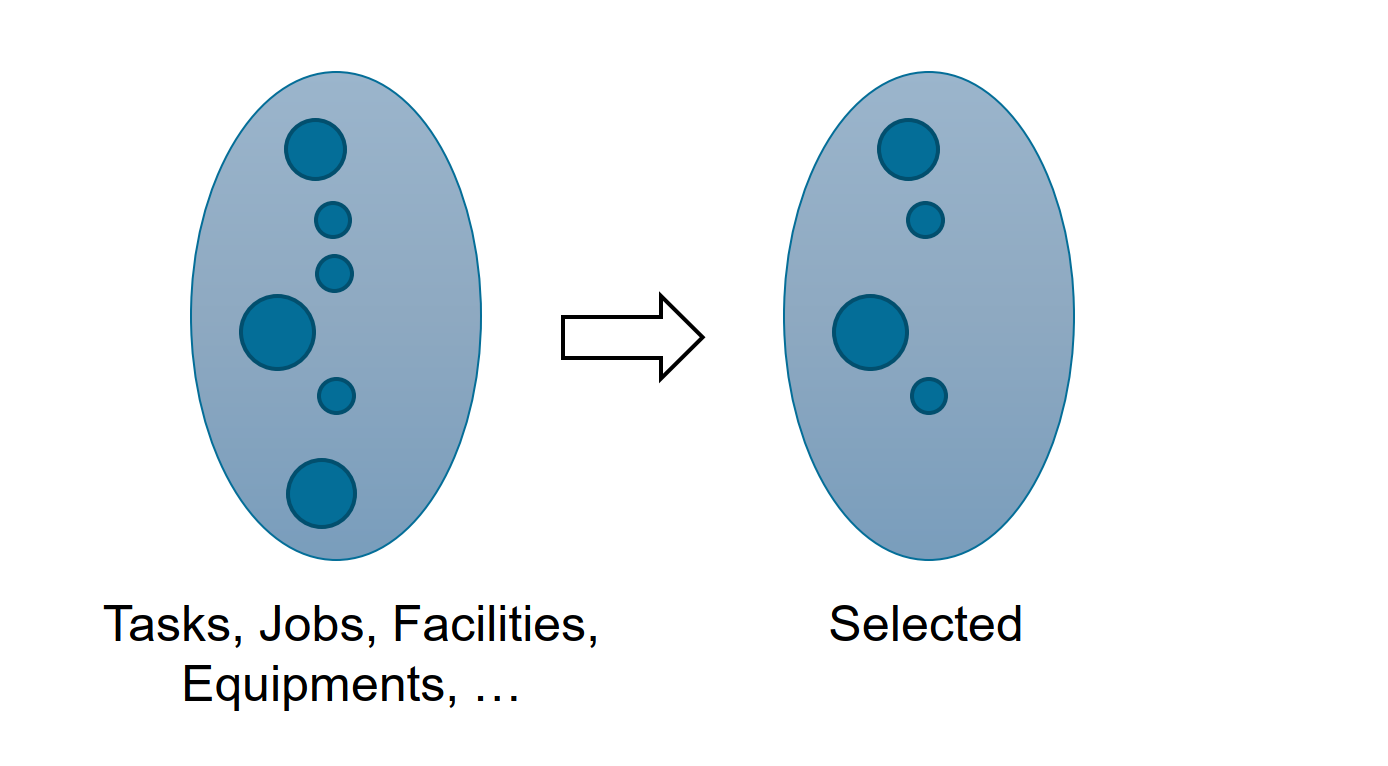
Well-known problems: knapsack problem (KSP)

Grouping problems

Solving grouping problems generally requires to find a subset of the powerset of all items. For instance, consider the task of coloring a graph where each node should be colored such that all adjacent nodes have different color. This is equivalent to identifying a partition of the nodes. Restrictions such as the minimal or maximal number of groups, or minimum and maximal number of items per group are quite common in practice.

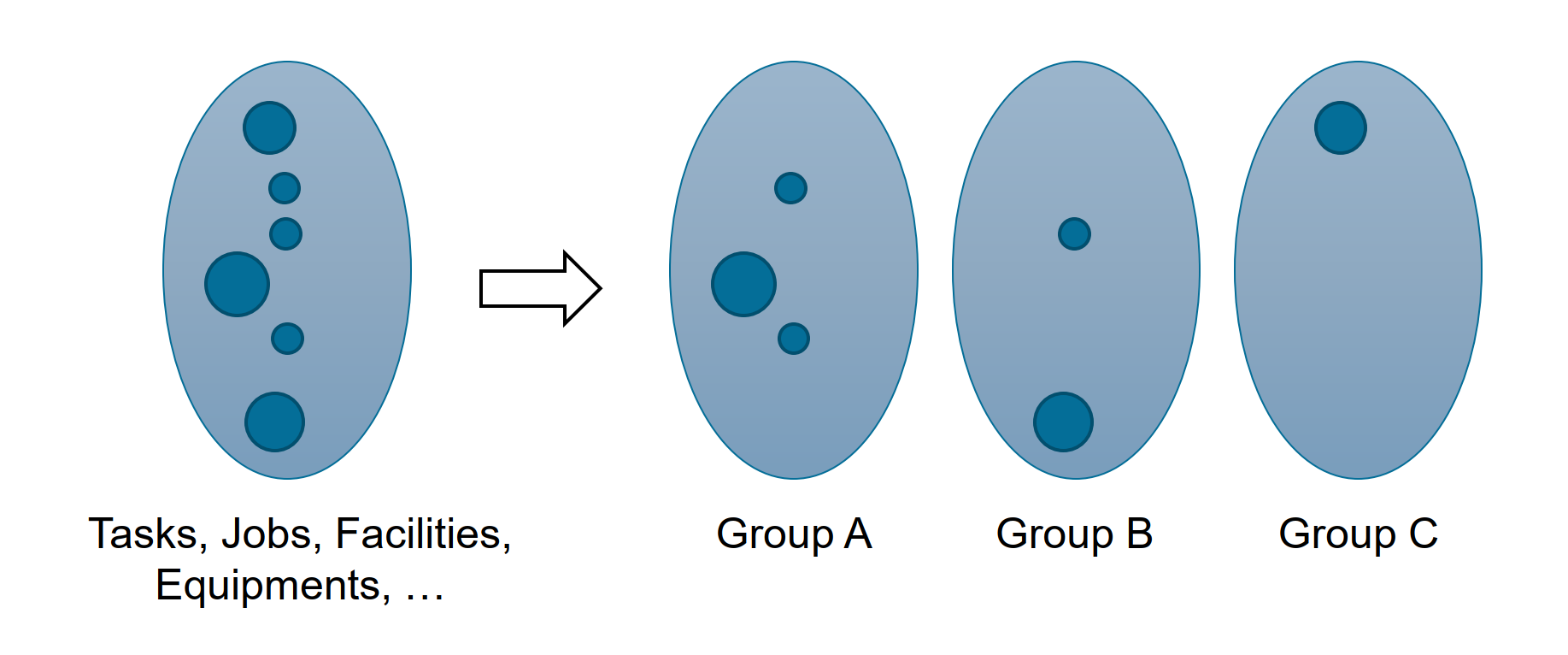
Well-known problems: graph coloring problem (GCP)

Combined problems

Often real-world and pratical problems may also be described as a combination of e.g. ordering and grouping. Consider for instance, the delivery of goods from a central warehouse to several retailing locations. The locations can be grouped into tours and within each group a tour, i.e., a sequence of locations, needs to be identified. Identifiying high quality solutions to such problems efficiently presents many challenges.

Well-known problems: vehicle routing problem (VRP), location routing problem (LRP), traveling thief problem (TTP)

Mathematical Programming

Many optimization problems can be formulated as mathematical programs, e.g., mixed integer programming (MIP) and solved with commercial off the shelf software in reasonable time even for larger dimensions thanks to advances in solver technology and a strong increase in the availability of computational power. We investigate the use of mathematical programming, devise a corresponding mathematical description of the problem and evaluate the use of exsiting solvers.

Simulation and optimization

Often the problem may not be described in closed mathematical form. There may be complex interrelationships and dynamics that need to be considered. In this case, the problem is described in form of a simulation model and simulation-based optimization is applied to identify good solutions. Solving such problems is computationally very expensive. We use parallel execution of many simulation models on distributed computers as well as population-based evolutionary algorithms to identify good solutions quickly. To improve convergence we investigate in the use of surrogate models, i.e., data-based models that approximate the simulation response, as well as custom variation operators to guide the search towards better solutions faster.

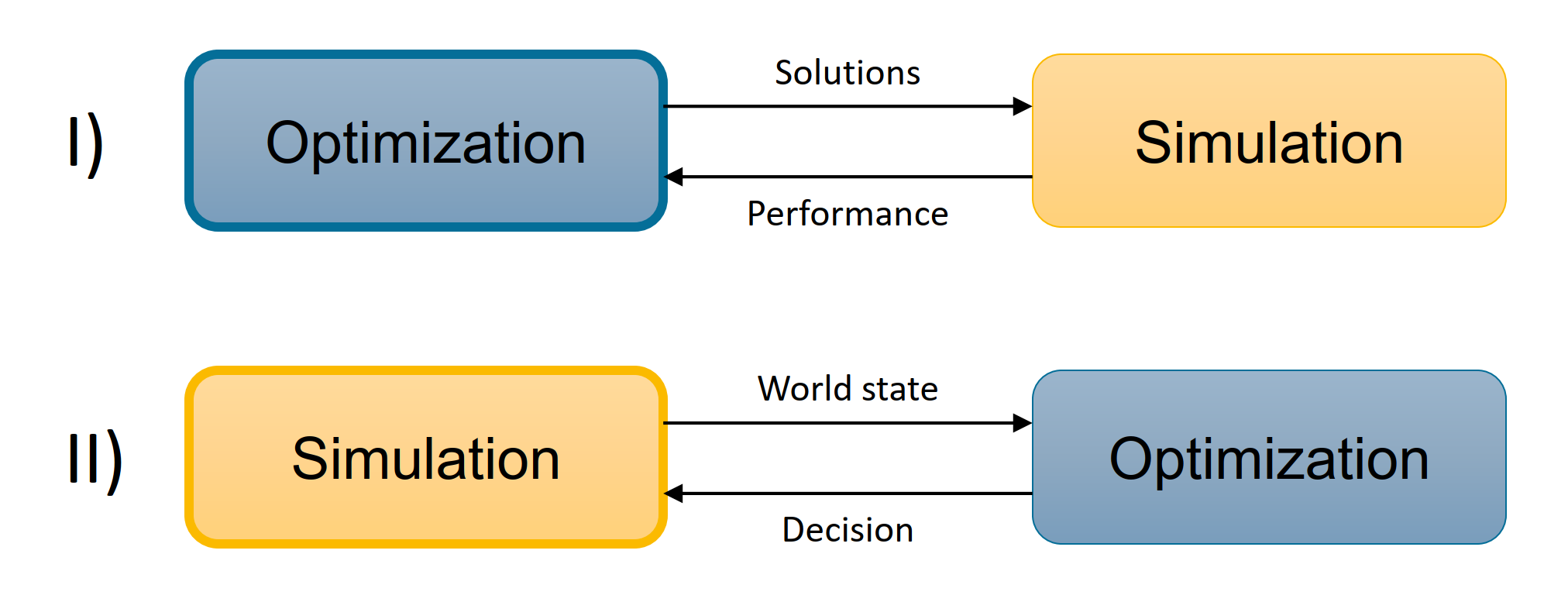
We distinguish between two types of simulation-based optimization as shown in the picture below. In case I), the optimization algorithm is the main driver. It computes new solutions and the simulation model is evaluating its quality, because the problem cannot be described in closed mathematical form. In case II), the simulation is the main driver. It calculates and updates a world state, but some decision need to be implemented and this needs to be provided by an optimization algorithm. Generally, such an algorithm is called policy in the second case. While in the first case the interest is to identify a good solution for a certain problem, the second case is more concerned about the dynamic effects that arise when implementing solutions from a certain policy.

Relevant projects

HOPL

Within the K-project "Heuristic Optimization in Production and Logistics" we investigated solution of combined problems. Together with the company partners voestalpine, Rosenbauer, carvatech, we described complex problems such as the stacking and batching within the hot storage area, as well as supply chain and production planning optimization problems. We extended HeuristicLab to allow describing problems by combining multiple solution representations (various vectors (binary, integer, real-valued, permutations, etc.) into one solution representation whereby for each representation variation operators would be applied independently. In addition, we devised a framework whereby solvers of sub-problems could interact with each other through an orchestration procedure that guides the search. We could among others successfully demonstrate this approach in solving the location routing problem, as well as the traveling thief problem.

LOISI

Within the project "Logistics Optimization in Steel Industries" we investigated the problems of scheduling WIP among the facilities, from casting to delivery. A mathematical model was devised based on the resource constraint project scheduling problem (RCPSP) which was formulated and compared for mixed integer programming solvers as well as for constraint programming solvers. The results showed that constraint programming was highly suitable to solve this problem. Additionally, we investigated the use of stacking problems in a further hotstorage environment.

SimGenOpt2

Within this FFG production of the future project we investigated the use of heuristic optimization techniques for optimizing production planning parameters which are used for instance in material requirements planning (MRP). An NSGA-II algorithm was adapted for a discrete encoding with custom variation operators that included domain specific knowledge. The algorithm identified a good approximation of the Pareto front ranging from solutions which favored low inventory costs to those that favored low tardiness costs. In addition, a mathematical model of the production planning task was devised for a battery production industrial case which calculated the master production schedule. The effect of the production planning parameters on the KPIs (inventory and tardiness costs) was simulated using an Anylogic-based simulation model.

Optimal Workforce

Within this production funded by the regional government of Upper Austria we investigated methods for the optimization of qualification matrices. A simulation model was created to describe two industrial production planning cases arising out of the electronics industry. An NSGA-II algorithm with custom solution encoding was applied to approximate the Pareto front consisting of solutions with high service levels to those with low number of total qualifications. The solutions have been analyzed together with the industry experts and recommendations were given on the qualification strategy for an improvement to service levels.

JRZ adaptOp

The Josef Ressel center for adaptive optimization in dynamic environments considers many problems that arise when the world changes dynamically. Solutions need to be constantly updated to the changing situations and feedback between environment and solver has to be considered. While the problems solved within JRZ adaptOp are often combinatorial, the topic of dynamic optimization deserves its own section on our site.

Selected publications

Karder, J. A., Beham, A., Hauder, V., Altendorfer, K., & Affenzeller, M. (2021). Simulation-based optimisation for worker cross-training. International Journal of Simulation and Process Modelling , 16(3), 185-194. doi:10.1504/IJSPM.2021.117309.

Sybilska, A., Słonina, M., Lejba, P., Lech, G., Karder, J. A., Suchodolski, T., Wagner, S., Sybilski, P., & Mancas, A. (2021). WebPlan - web-based sensor scheduling tool. Paper presented at 8th European Conference on Space Debris. https://conference.sdo.esoc.esa.int/proceedings/sdc8/paper/105.

Hauder, V., Beham, A., Leitner, S. J., Parragh, S., & Affenzeller, M. (2020). Resource-constrained multi-project scheduling with activity and time flexibility. Computers and Industrial Engineering, 150, [106857]. doi:10.1016/j.cie.2020.106857.

Altendorfer, K., Schober, A., Karder, J., & Beham, A. (2020). Service level improvement due to worker cross training with stochastic worker absence. International Journal of Production Research, 59(14), 4416-4433. doi:10.1080/00207543.2020.1764126.

Beham, A. (2019). Fitness Landscape Analysis and Algorithm Selection for Assignment Problems. PhD Thesis, Johannes Kepler University Linz.

Hauder, V., Karder, J., Beham, A., Wagner, S., & Affenzeller, M. (2018). A general solution approach for the location routing problem. In R. Moreno-Diaz, A. Quesada-Arencibia, & F. Pichler (Eds.), Computer Aided Systems Theory – EUROCAST 2017 - 16th International Conference, Revised Selected Papers (pp. 257-265). (Lecture Notes in Computer Science Vol. 10671 LNCS). Springer. doi:10.1007/978-3-319-74718-7_31.

Beham, A., Wagner, S., & Affenzeller, M. (2018). Algorithm selection on generalized quadratic assignment problem landscapes. In GECCO 2018 - Proceedings of the 2018 Genetic and Evolutionary Computation Conference (pp. 253-260). Association for Computing Machinery, Inc. doi:10.1145/3205455.3205585.

Raggl, S. J., Beham, A., Wagner, S., & Affenzeller, M. (2018). Analysing a hybrid model-based evolutionary algorithm for a hard grouping problem. In R. Moreno-Diaz, A. Quesada-Arencibia, & F. Pichler (Eds.), Computer Aided Systems Theory – EUROCAST 2017 - 16th International Conference, Revised Selected Papers (pp. 347-354). (Lecture Notes in Computer Science Vol. 10671 LNCS). Springer. doi:10.1007/978-3-319-74718-7_42.

Raggl, S. J., Beham, A., Hauder, V., Wagner, S., & Affenzeller, M. (2018). Discrete real-world problems in a black-box optimization benchmark. In GECCO 2018 Companion - Proceedings of the 2018 Genetic and Evolutionary Computation Conference Companion (pp. 1745-1752). Association for Computing Machinery, Inc. doi:10.1145/3205651.3208280.

Tricoire, F., Scagnetti, J., & Beham, A. (2018). New insights on the block relocation problem. Computers & Operations Research, 89, 127-139. doi:10.1016/j.cor.2017.08.010.

Raggl, S. J., Beham, A., Tricoire, F., & Affenzeller, M. (2018). Solving a Real World Steel Stacking Problem. International Journal of Service and Computing Oriented Manufacturing, 3(2). doi:10.1504/IJSCOM.2018.091621.

Karder, J., Beham, A., Wagner, S., & Affenzeller, M. (2018). Solving the traveling thief problem using orchestration in optimization networks. In R. Moreno-Diaz, A. Quesada-Arencibia, & F. Pichler (Eds.), Computer Aided Systems Theory – EUROCAST 2017 - 16th International Conference, Revised Selected Papers (pp. 307-315). (Lecture Notes in Computer Science Vol. 10671 LNCS). Springer. doi:10.1007/978-3-319-74718-7_37.

Karder, J., Scheibenpflug, A., Beham, A., Wagner, S., & Affenzeller, M. (2017). Extending Sim# for simulation-based optimisation of Semi-Automated machinery. International Journal of Simulation and Process Modelling, 12(6), 485-497. doi:10.1504/IJSPM.2017.089634.

Beham, A., Affenzeller, M., & Wagner, S. (2017). Instance-based algorithm selection on quadratic assignment problem landscapes. In GECCO 2017 - Proceedings of the Genetic and Evolutionary Computation Conference Companion (pp. 1471-1478). ACM Sigevo. doi:10.1145/3067695.3082513

Hauder, V., Beham, A., Wagner, S., & Affenzeller, M. (2017). Optimization networks for real-world production and logistics problems. In GECCO 2017 - Proceedings of the Genetic and Evolutionary Computation Conference Companion (pp. 1411-1414). Association for Computing Machinery, Inc. doi:10.1145/3067695.3092959.

Karder, J., Scheibenpflug, A., Wagner, S., & Affenzeller, M. (2016). Generation of dispatching rules for job sequencing in singlemachine environments. In A. G. Bruzzone, E. Jimenez, L. S. Louca, L. Zhang, & F. Longo (Eds.), 28th European Modeling and Simulation Symposium, EMSS 2016 (pp. 117-121). DIME UNIVERSITY OF GENOA.

Beham, A., Scagnetti, J., Kommenda, M., Wagner, S., Winkler, S., & Affenzeller, M. (2015). Optimization Strategies for Integrated Knapsack and Traveling Salesman Problems. In F. Pichler, R. Moreno-Díaz, & A. Quesada-Arencibia (Eds.), Computer Aided Systems Theory – EUROCAST 2015 - 15th International Conference, Revised Selected Papers (pp. 359-366). (Lecture Notes in Computer Science Vol. 9520). Springer. doi:10.1007/978-3-319-27340-2_45.